Mathematical Induction

(C) 1999 Daniel Kovacs

In any science, people have new ideas and concepts, which may or may not be correct. This is especially true in Mathematics, and over the years, mathematicians have come up with ways to verify their formulas. One such method is called Mathematical Induction.

How it works ...

For this example, I will use the following equasion:

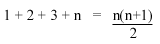
The sum of all integers

If you recognise this equasion, you will see that it is the sum of integers. The first step in prooving a formula by induction is to see if the formula works for the value 1. (I will say the formula = P, and then the we will solve for P(1)):

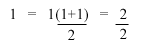
As you can see, 2/2 = 1, so the formula works for P(1). Now that this is established, it is nessesary to show the same formula with K factored in. This is where most people get confused, but it is really quite simple. Here is what you get:

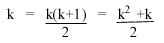
The formula works for k, so the formula must also work for k+1 (this is nessesary to proove that this success is not just arbitrary, but works for all of Z). To do this, substitute k+1 into the origonal formula, and simplify it:

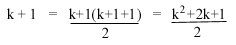
The formula works for k+1, and this is what we needed to show. That's all there is too it! If you didn't get this answer, you should practice some algebra. If so, that's very good! This is what is called an Elementary Method of Proof, and is usually taught to University Students taking Discrete Mathematics. Induction is essential knowledge in upper-year courses, especially for those in Mathematics and Computer Science.

Back to index.