For the comparison operations, Set on Less Than (SLT) and
Set on Less Than Unsigned (SLTU), we wish to determine whether
the input A is less than the input B. If it is,
we wish to set the result to X"00000001". If it is not,
we wish to set the result to X"00000000".
Let's start by looking at the calculation we wish to perform:
A < B. Using a little simple algebra, this expression
can be rewritten as A - B < 0. If we were to subtract
B from A, then all that would remain is the
relatively trivial matter of determining whether the result
is less than zero. Instead of a large comparator which will
consume a number of gates, we can once again reuse our single
adder with a minimal amount of logic looking at the output.
First, we must make sure that our existing Arithmetic
sub-block is performing a subtraction operation. This will
occur when ALUOp(1 DOWNTO 0) is either "10" or "11".
fortunately, we only have two comparison operations to perform.
SLT will require a signed subtraction, thus it will
be encoded as ALUOp(1 DOWNTO 0) = "10". SLTU
will require an unsigned subtraction, thus it will be
encoded as ALUOp(1 DOWNTO 0) = "11". The remaining
two encodings for this sub-block will be undefined.
Now, the question is how do we determine if the result is
less than zero based on the four inputs which we have
defined to the Comparison sub-block: CarryOut
from the subtractor, Bit 31 of the subtractor result
ArithmeticR, Bit 31 of the input A,
and Bit 31 of the input B.
Let's start with the Signed version. There are four
possible combinations of the signs of the inputs: both
are positive; both are negative; A is positive
and B is negative; A is negative and
B is positive. When the signs of the inputs
are different, our problem is trivial. If A
is negative and B positive, then A MUST
be less than B. Conversely, if A is
positive and B is negative then A
CAN NEVER be less than B. When the
inputs have the same sign we need to look at the result
of the signed subtraction. Two inputs with the same
sign can never cause an overflow in subtraction, so
we do not have to concern ourselves with an incorrect
answer due to that. If the inputs are of the same sign,
then whenever A is smaller than B the
result of subtracting A - B MUST be a
negative number. So, if the sign of the result,
SignR, is negative we have A < B
and if it is positive or zero then we have
A ≥ B.
For the Unsigned version of the comparison we have a simple test. In unsigned representation, A and B are both positive numbers. Subtracting two positive numbers will result in a positive number if A > B or a negative number if A < B. However, we cannot represent a negative number with an Unsigned integer: if we try we will have an overflow condition. Overflow for unsigned subtraction means that the result is a negative number (it is impossible to subtract two unsigned numbers and get a result too large to represent). We can test for the occurence of overflow in unsigned subtraction by looking at the Carry Out of the most significant bit. In unsigned addition, the existence of a Carry Out indicates overflow. In unsigned subtraction, however, the situation is reversed: Carry Out high is the normal state and Carry Out low indicates overflow. Thus, since we are performing unsigned subtraction in our SLTU, if there is no Carry Out, then we had an overflow and A - B is less than zero and A < B is true. If there is a Carry Out, then A - B is greater than zero and A < B is false.
Since we are only concerned with four input bits to
determine our output, we will be implementing the
Comparison sub-block by creating a Truth
Table view.
First, you need to open a new Truth Table view for the Comparison sub-block. Do this by opening the ALU block diagram, double-click on the Comparison sub-block, select the Graphical View category and select Truth Table from the list box. Click Next and click Finish.
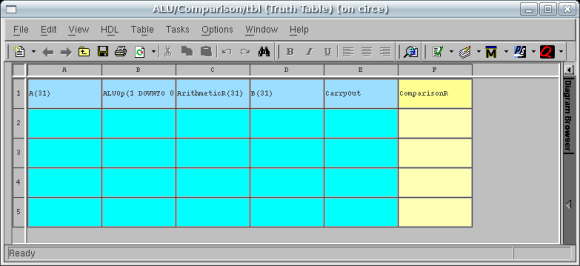
The Truth Table view window will appear similar to the
figure below:

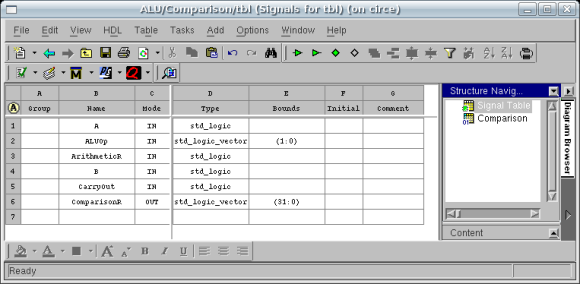
First, relabel the columns in the following
order: ALUOp (1 DOWNTO 0), A, B, ArithmeticR,
CarryOut, ComparisonR. In order to relabel
a column, left-click and type in the new value.
This is very important to do! Unfortunately,
the truth table keeps the name of the signals
coming in but sees them differently. Click
the Diagram Browser at the right of
the truth table to observe the Signal
Table. As you can see from the figure
below, A(31) is now just A.
The same applies to ArithmeticR and B.
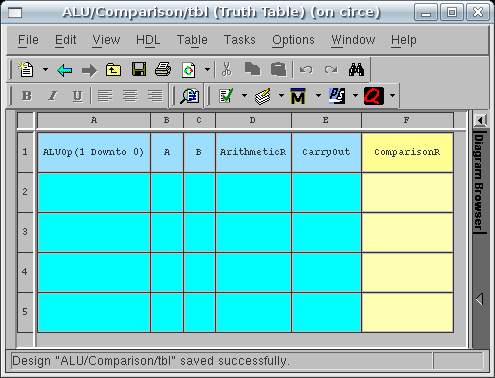
Return to your Truth Table by clicking on
Comparison. You may resize the rows and
columns of the Truth Table by moving
the pointer over the lines separating the row and
column headers (which are in gray), left-clicking,
and dragging to the desired height or width just
like in a spreadsheet program. Resize the
A, B, ArithmeticR, and
CarryOut columns so that the signal
names just fit. Now make the ComparisonR
column much larger because it will be holding a
32-bit wide vector. You may also center the
data in your rows and columns by selecting
all (CTRL + A) and click the Center
button,  Your view should look something like the figure
below:
Your view should look something like the figure
below:
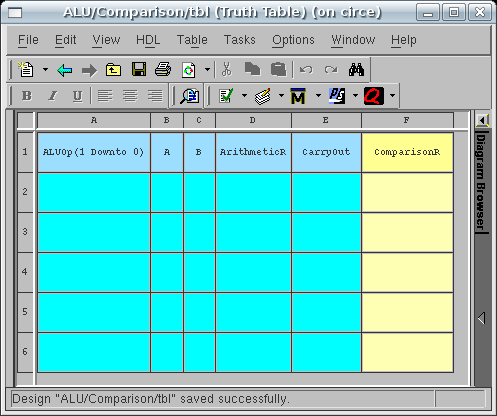
We will need more than four rows in this Truth
Table. A row can be added, by right-clicking
anywhere over the table and selecting Add Row
from the pop-up menu. Add 1 more row
so that your table looks like the figure below:
Now we will start to add information to the table.
Values are entered by left-clicking on the
appropriate cell and typing in the data.
Don't Care values are specified by
leaving a cell empty. Don't care's are useful to
shorten the length of the table when a particular
entry does not depend on the state of one or more
of the inputs. For example, to completely specify
the truth table for our design with six bits of
input we would need 64 rows but by using don't
cares we can reduce that to 5.
This reduction in the truth table is achieved by a
combination of matching only outcomes with a TRUE
output(X"00000001") and don't cares for the rest of
the input combinations. The one row of don't cares
for a FALSE output(X"00000000") will save the
user from 60 rows of unnecessary logic.
Let's start with the signed comparison operation, SLT, which is performed when ALUOp is equal to "10". Remember from above that there were three possible situations: A and B have the same sign, A is positive and B is negative, or A is negative and B is positive.
Let's start with the case of both inputs having the same
sign. This occurs when A(31) = '0' and B(31) = '0'
or A(31) = '1' and B(31) = '1'. In each
case all we need to do is look at the sign of the result,
ArithmeticR(31). If ArithmeticR(31) = '0'
then the result is positive and we want to output FALSE,
or X"00000000". We can skip adding this entry into the
truth table since it's FALSE. If ArithmeticR(31) = '1'
then the result is negative and the output is TRUE,
or X"00000001". We now have two TRUE possiblities
that we can now add to the truth table. Your Truth
Table should resemble the figure below:
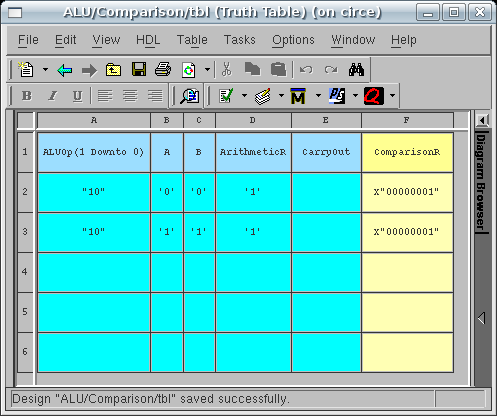
Now we have two cases left. When A(31) = '0' and
B(31) = '1' we have A as a positive number and
B as a negative number, meaning that A must be
greater than B and our result is always going to be
false. This means that we don't care what the value of
ArithmeticR(31) or CarryOut is. Conversely,
when A(31) = '1' and B(31) = '0' then
A is negative and B is positive and A
must be less than B so our result is always true.
Since we're only adding the TRUE possiblities, we now
have one more line to add to the table. Your Truth Table
should resemble the figure below:
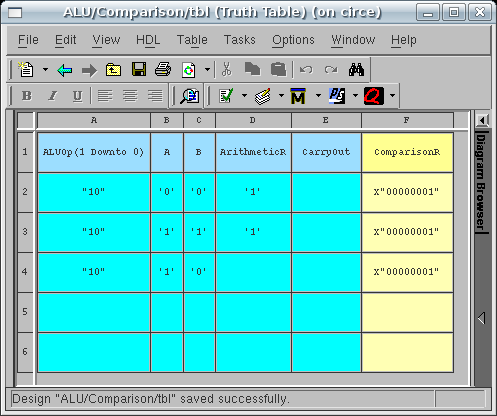
We have now completely specified the behavior of the table
for SLT, or ALUOp(1 DOWNTO 0) = "10".
We have one line left to fill in in the table which will specify the last 16 cases that correspond to ALUOp(1 DOWNTO 0) = "11", or Set on Less than Unsigned. Remember from above that we can test for A < B unsigned by performing an unsigned subtraction and checking for an overflow indicated by examining carry out from the most significant bit of the adder. So, if we are performing SLTU all we need to look at is the CarryOut signal. If CarryOut = '1', then we did not have overflow, hence A - B > 0 and we report FALSE. If CarryOut = '0', then we have had an overflow and A - B < 0 so we report TRUE. Our one line of logic has been implemented in the table shown in the figure below:
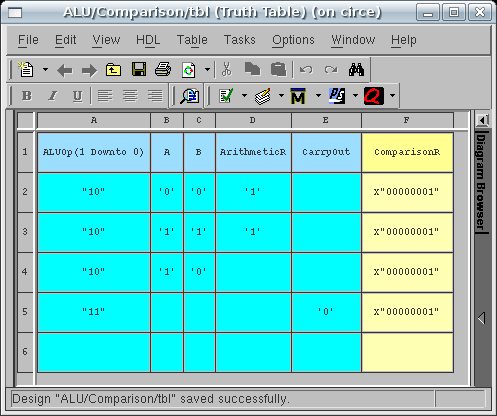
The last step we have to complete in this table is the
don't care for any other combination of inputs. This
can be done by leaving all inputs blank and setting
the output to the FALSE value. Your Truth
Table should resemble the figure below:
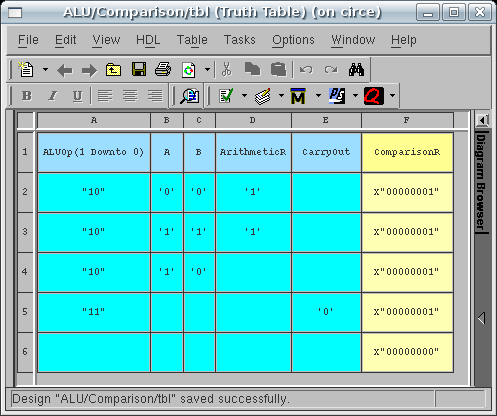
The Comparison sub-block is difficult to fully test
in a stand-alone manner due to the fact that it requires
the Arithmetic sub-block to function correctly.
However, it is also a relatively simple sub-block, so we
will put off testing its functionality for now and verify
that it works correctly when we are simulating the entire
ALU.
Below is the generated HDL for the Truth Table
-- VHDL Entity ALU.Comparison.interface
--
-- Created:
-- by - elenis.student (circe)
-- at - 18:59:03 01/09/07
--
-- Generated by Mentor Graphics' HDL Designer(TM) 2005.3 (Build 75)
--
LIBRARY ieee;
USE ieee.std_logic_1164.all;
USE ieee.std_logic_arith.all;
ENTITY Comparison IS
PORT(
A : IN std_logic;
ALUOp : IN std_logic_vector (1 DOWNTO 0);
ArithmeticR : IN std_logic;
B : IN std_logic;
CarryOut : IN std_logic;
ComparisonR : OUT std_logic_vector (31 DOWNTO 0)
);
-- Declarations
END Comparison ;
--
-- VHDL Architecture ALU.Comparison.tbl
--
-- Created:
-- by - elenis.student (circe)
-- at - 18:59:03 01/09/07
--
-- Generated by Mentor Graphics' HDL Designer(TM) 2005.3 (Build 75)
--
LIBRARY ieee;
USE ieee.std_logic_1164.all;
USE ieee.std_logic_arith.all;
ARCHITECTURE tbl OF Comparison IS
-- Architecture declarations
BEGIN
-----------------------------------------------------------------
truth_process_proc: PROCESS(A, ALUOp, ArithmeticR, B, CarryOut)
-----------------------------------------------------------------
BEGIN
-- Block 1
IF (ALUOp(1 Downto 0) = "10") AND (A = '0') AND (B = '0') AND
(ArithmeticR = '1') THEN
ComparisonR <= X"00000001";
ELSIF (ALUOp(1 Downto 0) = "10") AND (A = '1') AND (B = '1')
AND (ArithmeticR = '1') THEN
ComparisonR <= X"00000001";
ELSIF (ALUOp(1 Downto 0) = "10") AND (A = '1') AND (B = '0') THEN
ComparisonR <= X"00000001";
ELSIF (ALUOp(1 Downto 0) = "11") AND (CarryOut = '0') THEN
ComparisonR <= X"00000001";
ELSE
ComparisonR <= X"00000000";
END IF;
END PROCESS truth_process_proc;
-- Architecture concurrent statements
END tbl;
|
Now that you have finished defining the last of the
Operation sub-blocks, all that is left to
complete the ALU is the Mux.