Lab 09
Adjacency Matrix Graph
Objective:
Create a class which constructs an adjacency matrix representation of a graph and performs a few graph operations.
Lab Solution
Requirements:
- Functionality. (80pts)
- No Syntax, Major Run-Time, or Major Logic Errors. (80pts*)
- *Code that cannot be compiled due to syntax errors is nonfunctional code and will receive no points for this entire section.
- *Code that cannot be executed or tested due to major run-time or logic errors is nonfunctional code and will receive no points for this entire section.
- Set up the Project. (5pts)
- First download the driver file and include it in
your project.
- Create a class and name
it, exactly, AdjMatrixGraph.
- Do not modify the
provided driver or text file.
- All must apply for full credit.
- Write the following Properties (10pts)
- adjMatrix: this is a 2D Array of type double that is always square. The length and width are always equal to the number of vertices. The indices correspond to the unique name of the vertex and the decimal values correspond to the distance from one vertex to another. We assume if this value is 0, then there is no edge.
- DEF_VERT_COUNT: is a constant, static whole number value set to 10.
- Write two Constructors (5pts)
- Default (1pt)
- Constructs the adjMatrix using the default vertex count of 10.
- Parameterized (4pts)
- An integer “size” must be checked and then used to construct the adjMatrix.
- Write method addEdge (10pts)
- This method must be provided the index of the “from Vertex”, the index of the “to Vertex”, and the weight (distance) of a decimal type.
- This method must check if the indices of the “from Vertex” and the “to Vertex” are valid values.
- Assuming they are valid, then the method must update the adjMatrix’s value in the corresponding cell.
- All must apply for full credit.
- Write method printAdjMatrix (5pts)
- Prints the values of the 2D array line-by-line.
- All must apply for full credit.
- Write method printDFS (10pts)
- This method prints the depth first search starting from the first vertex (index == 0) to all reachable vertices.
- Each Vertex must have its unique name (its index) printed in visitation order.
- Ties are broken by selecting the lesser of the two indices (IE Vertex 2 is visited before Vertex 4).
- You may use any data
structure to keep track of visited vertices. This includes anything in “import
java.util.*” or any previously created data structures.
- All must apply for full credit.
- Write method printDFSFrom (10pts)
- This method must be provided an integer value which corresponds to the vertex number.
- Assume that index 0 is the first vertex.
- It must print the depth first search starting from that vertex to all reachable vertices.
- Each Vertex must have its
unique name (its index) printed in visitation order.
- Ties are broken by selecting the lesser of the two indices (IE Vertex 2 is visited before Vertex 4).
- You may use any data structure to keep track of visited vertices. This includes anything in “import java.util.*” or any previously created data structures.
- All must apply for full credit.
- Write method printBFS (10pts)
- This method prints the breadth first search starting from the first vertex (index == 0) to all reachable vertices.
- Each Vertex must have its
unique name (its index) printed in visitation order.
- Ties are broken by selecting the lesser of the two indices (IE Vertex 2 is visited before Vertex 4).
- You may use any data
structure to keep track of visited vertices. This includes anything in “import
java.util.*” or any previously created data structures.
- All must apply for full credit.
- Write method printBFSFrom (10pts)
- This method must be
provided an integer value which corresponds to the vertex number.
- Assume that index 0 is
the first vertex.
- It must print the depth
first search starting from that vertex to all reachable vertices.
- Each Vertex must have its
unique name (its index) printed in visitation order.
- Ties are broken by selecting the lesser of the two indices (IE Vertex 2 is visited before Vertex 4).
- You may use any data
structure to keep track of visited vertices. This includes anything in “import
java.util.*” or any previously created data structures.
- All must apply for full credit.
- Coding Style. (10pts)
- Code functionality
organized within multiple methods other than the main method, and methods
organized within multiple classes where appropriate. (5pts)
- Readable Code (5pts)
- Meaningful identifiers
for data and methods.
- Proper indentation that
clearly identifies statements within the body of a class, a method, a
branching statement, a loop statement, etc.
- All the above must apply
for full credit.
- Comments. (10pts)
- Your name in the file.
(5pts)
- At least 5 meaningful comments in addition to your name. These must describe the function of the code it is near. (5pts)
The provided tester uses the following Graph for reference.
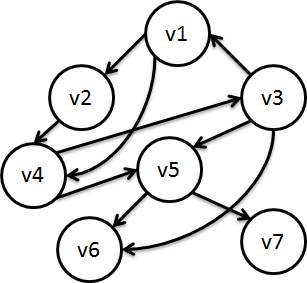
Example Dialog:
*The following
Example Dialog demonstrates the interactions between a user and ONE possible
implementation of the required software’s front-end / user interface. The
software’s front-end / user interface may be implemented in MANY different
ways and will receive full credit as long as it meets the most minimal of
the above requirements. While you may use the example dialog as a guide, it is
strongly encouraged to create the front-end / user interface in your own way. *
|
Key |
|
|
Unhighlighted Text |
Program’s Output |
|
Highlighted
Text |
User’s
Input |
-------------------------------------
TEST: Making graph with 7 Vertices
-------------------------------------
Graph is not null? true
-------------------------------------
TEST: Adding edges
-------------------------------------
10 Edges have been added.
-------------------------------------
TEST: Print ADJMatrix
-------------------------------------
0.0 1.0 0.0 1.0 0.0 0.0 0.0
0.0 0.0 0.0 1.0 0.0 0.0 0.0
1.0 0.0 0.0 0.0 1.0 1.0 0.0
0.0 0.0 1.0 0.0 1.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 1.0 1.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0
-------------------------------------
TEST: Print DFS from Vertex 1 (index
0)
-------------------------------------
0
1
3
2
4
5
6
-------------------------------------
TEST: Print BFS from Vertex 1 (index
0)
-------------------------------------
0
1
3
2
4
5
6
-------------------------------------
TEST: Print DFS from Vertex 5 (index
4)
-------------------------------------
4
5
6
-------------------------------------
TEST: Printing BFS from Vertex 3
(index 2)
-------------------------------------
2
0
4
5
1
3
6
Lab Report Questions:
- Create a section named “Problem” and describe this lab’s problem in your own words. (10pts).
- Create a section named “Solution Description” and describe how the code solves the problem in your own words. (10pts).
- Create a section named “Problems Encountered” and describe the various syntax, run-time, and logic errors that were encountered while implementing the solution. (10pts).
- Describe the process of DFS in your own words. (10pts).
- Describe the process of BFS in your own words. (10pts).
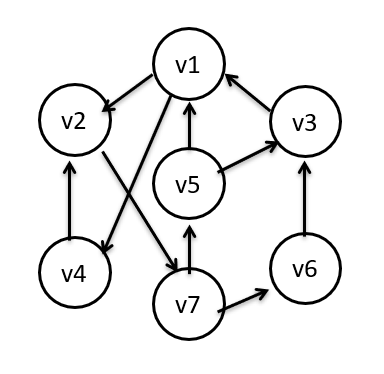
- Using the above graph, create a corresponding adjacency matrix. Assume
the rows are “from” vertices and the columns are “to” vertices.
- Using the above graph, describe the DFS starting from vertex “v5”. This
must include all uniquely visited vertices (no duplicates) in DFS
order. Ties are broken based on the lesser of the two values (IE
Vertex 2 is visited before Vertex 4).
- Using the above graph, describe the BFS starting from vertex “v5”. This
must include all uniquely visited vertices (no duplicates) in BFS
order. Ties are broken based on the lesser of the two values (IE
Vertex 2 is visited before Vertex 4).
- Using the above graph, describe the DFS starting from vertex “v2”. This
must include all uniquely visited vertices (no duplicates) in DFS
order. Ties are broken based on the lesser of the two values (IE
Vertex 2 is visited before Vertex 4).
- Using the above graph, describe the BFS starting from vertex “v2”. This
must include all uniquely visited vertices (no duplicates) in BFS
order. Ties are broken based on the lesser of the two values (IE
Vertex 2 is visited before Vertex 4).
Finally:
- Upload the source code (.JAVA File Extension) to LabSolution09
- And written lab report
(DOC, .DOCX, or .PDF file extension) to LabReport09
- To Blackboard
- Following these instructions.
- If there are problems, then let the instructor know as soon as possible.