Medium-Scale Integrated Circuits
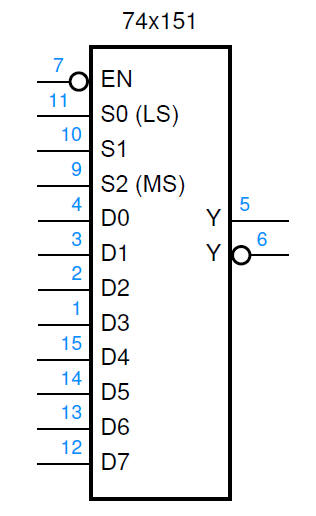
Using a 74LS151 (8-to-1 multiplexer) to Implement
a Function of Four Variables
- Group row 0 with row 1; 2 with 3,…, and 14 with 15.
- Connect the three most significant variables W,
X, and Y to select lines S2 (MS), S1, and S0 (preserve order of
significance).
- For each pair
of rows, compare the two function values to the Z column. Each input D0
to D7 must be one of 0, 1, Z, or Z′ as noted below.
- Enable the chip.
The function output is the MUX output, Y-out.
- F′ is available if needed.
|
Row |
W |
X |
Y |
Z |
F(W,X,Y,Z) |
Input |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
0 |
1 |
0 |
D0 = 0 |
|
2 |
0 |
0 |
1 |
0 |
0 |
|
|
3 |
0 |
0 |
1 |
1 |
1 |
D1 = Z |
|
4 |
0 |
1 |
0 |
0 |
1 |
|
|
5 |
0 |
1 |
0 |
1 |
0 |
D2 = Z’ |
|
6 |
0 |
1 |
1 |
0 |
1 |
|
|
7 |
0 |
1 |
1 |
1 |
1 |
D3 = 1 |
|
8 |
1 |
0 |
0 |
0 |
1 |
|
|
9 |
1 |
0 |
0 |
1 |
1 |
D4 = 1 |
|
10 |
1 |
0 |
1 |
0 |
1 |
|
|
11 |
1 |
0 |
1 |
1 |
0 |
D5 = Z’ |
|
12 |
1 |
1 |
0 |
0 |
0 |
|
|
13 |
1 |
1 |
0 |
1 |
1 |
D6 = Z |
|
14 |
1 |
1 |
1 |
0 |
0 |
|
|
15 |
1 |
1 |
1 |
1 |
0 |
D7 = 0 |
Using a
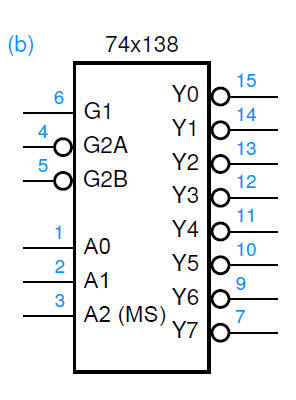
Decoder to Implement a Function
- Choose the version of
the function with the fewest min or max terms.
- When enabled, the active-low decoder shown below
generates max terms of the
address variables A2, A1, and A0.
For example, when A2, A1, and A0 = 1 0 0,
M4 is generated at Y4_L. In this
case, Y4_L = “0”; all other outputs are “1.”
- Use an external AND
gate to combine max terms.
- Use an external NAND
gate to combine min terms.
Decoder Example
1:
F(X, Y, Z) = PM(0, 2, 3, 5, 7) = Sm(1, 4, 6)
Enable the decoder.
Connect input variables X (MS), Y, and Z to address lines A2, A1, and
A0. NAND
decoder outputs 1, 4, 6 (this effectively OR’s the min terms of the same number
using DeMorgan’s Theorems.)
Decoder Example 2:
G(X, Y, Z) = PM(0, 3,
4)
Enable the decoder.
Connect input variables X (MS), Y, and Z to address lines A2 (MS), A1,
and A0. Use an AND
gate to combine decoder outputs 0, 3, 4 (the max terms).